[Softeer] S635

[Softeer]

Question

Language: Python

해당 문제는 각 노드에 대해 다른 노드 까지에 이른 최소 경로의 합을 구하는 유형의 문제이다. 하지만, 노드의 수가 굉장히 많기 때문에 아래와 같이 모든 노드에 대한 DFS/BFS을 수행하는 것은 시간 초과 문제를 발생한다.

실패 코드(시간 초과)

import sys
from collections import deque

def bfs(start):
    visited=[False]*(n_vertex+1)
    queue=deque([(start,0)])
    visited[start]=True
    sum_cost=0
    while queue:
        vertex,cost=queue.popleft()

        for adj_vertex, weight in graph[vertex]:
            if visited[adj_vertex]:
                continue
            
            visited[adj_vertex]=True
            queue.append((adj_vertex,cost+weight))
            sum_cost+=(cost+weight)
        
    return sum_cost

def solution():
    #distances=[[0]*(n_vertex+1) for _ in range(n_vertex+1)]

    for i in range(1,n_vertex+1):
        print(bfs(i))

if __name__ == "__main__":
    n_vertex=int(input())
    graph=[[] for _ in range(n_vertex+1)]

    for _ in range(n_vertex-1):
        v1,v2,weight=map(int,input().split())
        graph[v1].append((v2,weight))
        graph[v2].append((v1,weight))
    
    solution()

다행히도, 해당 문제는 노드와 노드를 잇는 경로가 무조건 1개만 존재하는 Tree 라는 점에서 DFS 횟수를 줄일 수 있다. subtree을 활용하여 subtree에 대한 거리합을 저장하므로써 반복 횟수를 줄인다.

tree

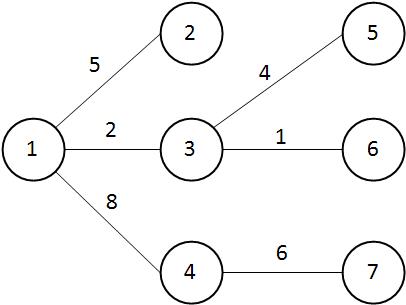
DFS 1 (Bottom-Up)

우선, Bottom-up 방식의 dfs 수행을 통해 각각의 노드를 subtree로 하는 subtree 개수 및, 해당 subtree에 대한 거리합을 구한다.

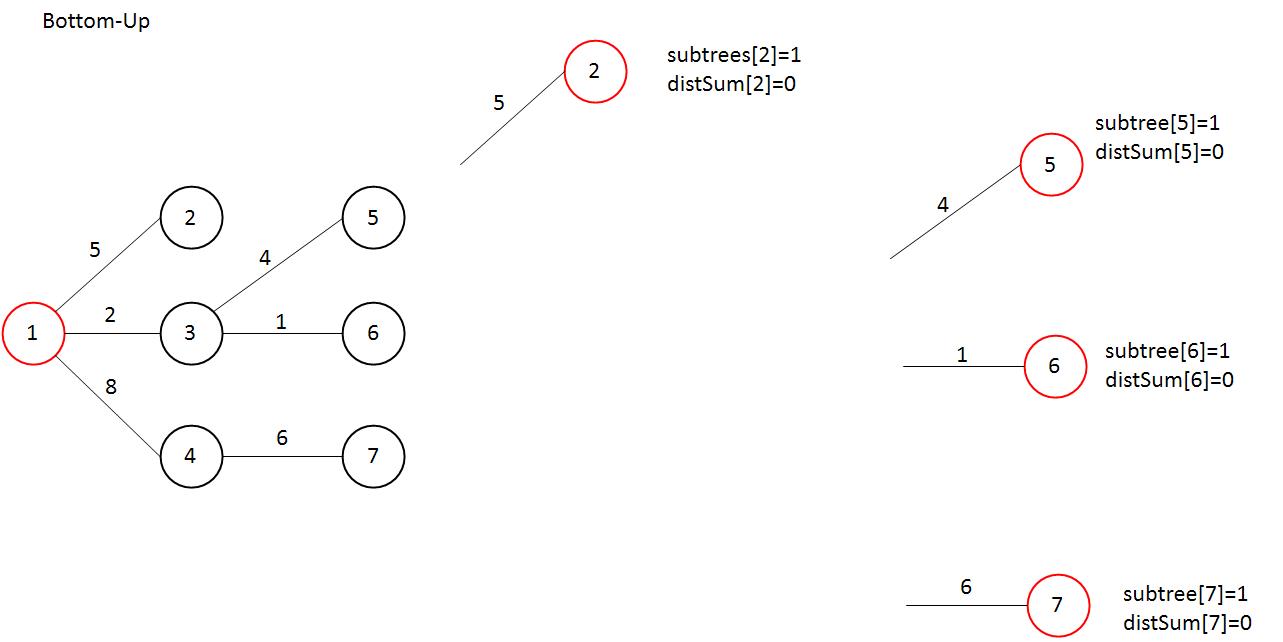
leaf node는 subTree개수는 1개, distSum은 자식 노드가 없으므로 0이다.

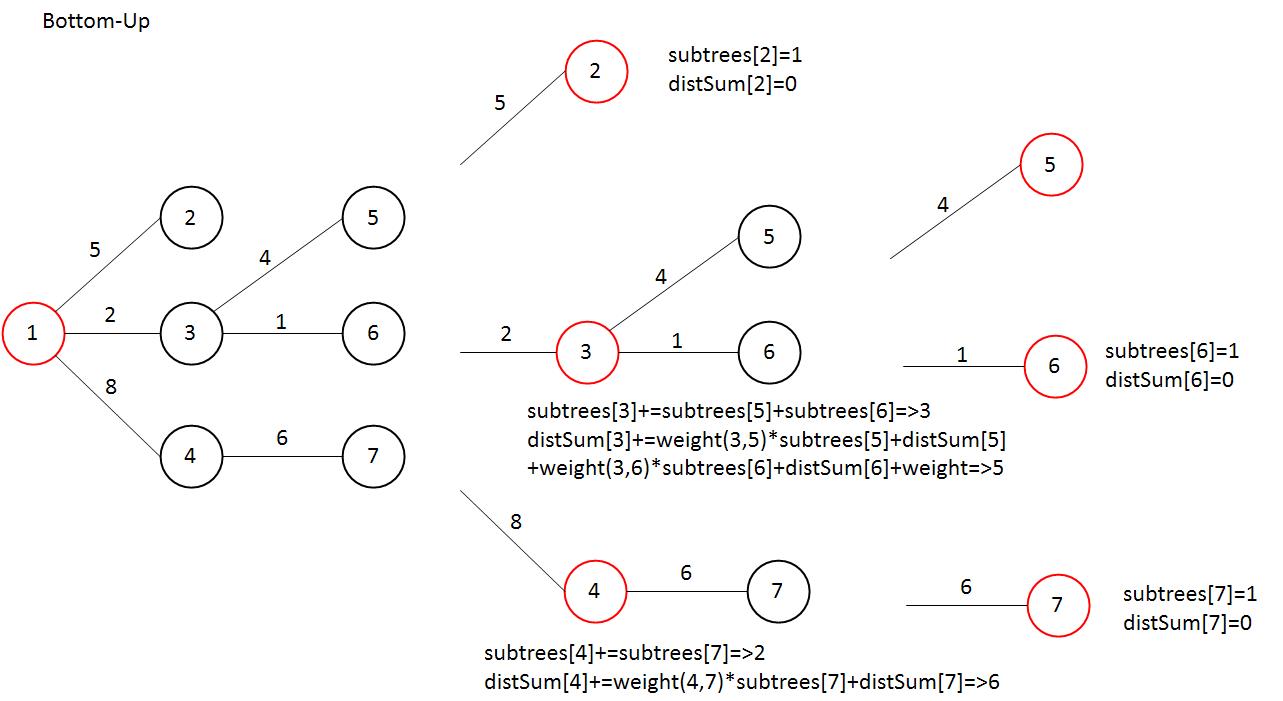
자식 노드를 1개 이상 갖는 노드에 대해 각각 아래의 연산을 진행하여 각 subTree에 대해 subTrees, distSum을 구한다.

subtrees[vertex]+=subtrees[adj_vertex]
distSum[vertex]+=(subtrees[adj_vertex]*weight + distSum[adj_vertex])

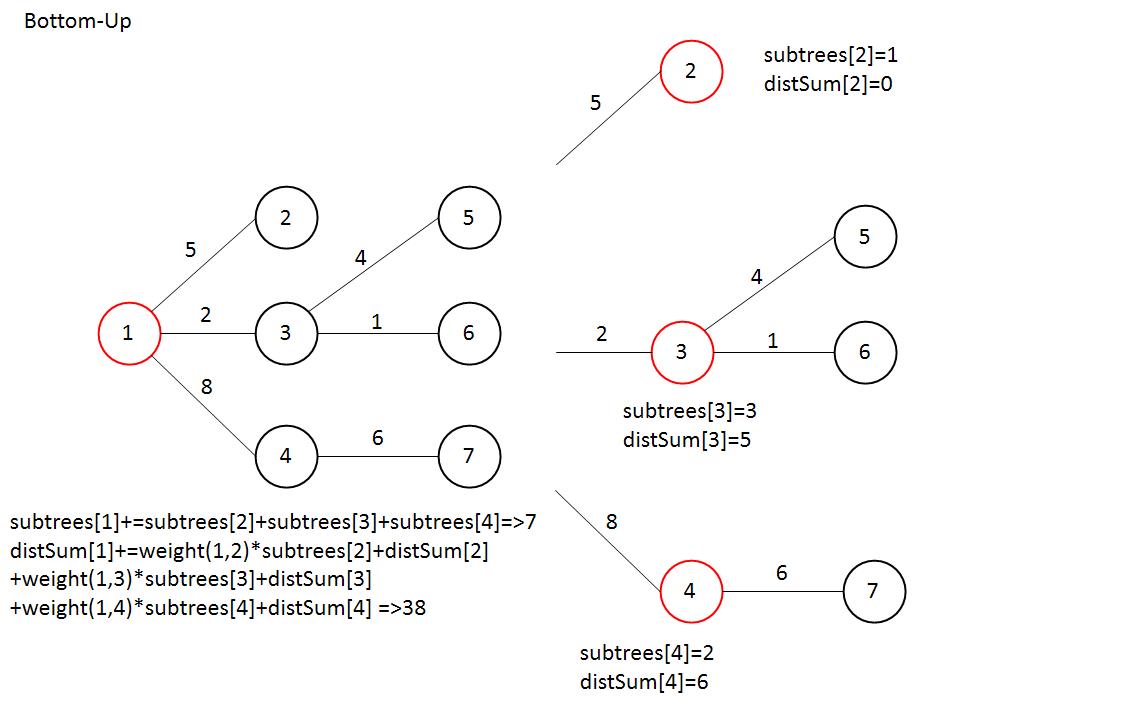
이렇게 하면 루트 노드 1를 기준으로한 모든 subTree에 대한 subtrees, distSum을 구할 수 있게 된다.

이제는, 각 노드에 대해 각각의 노드에 대한 이르는 경로의 거리합을 구하기 위해 Top-down DFS을 수행한다.

Top-Down

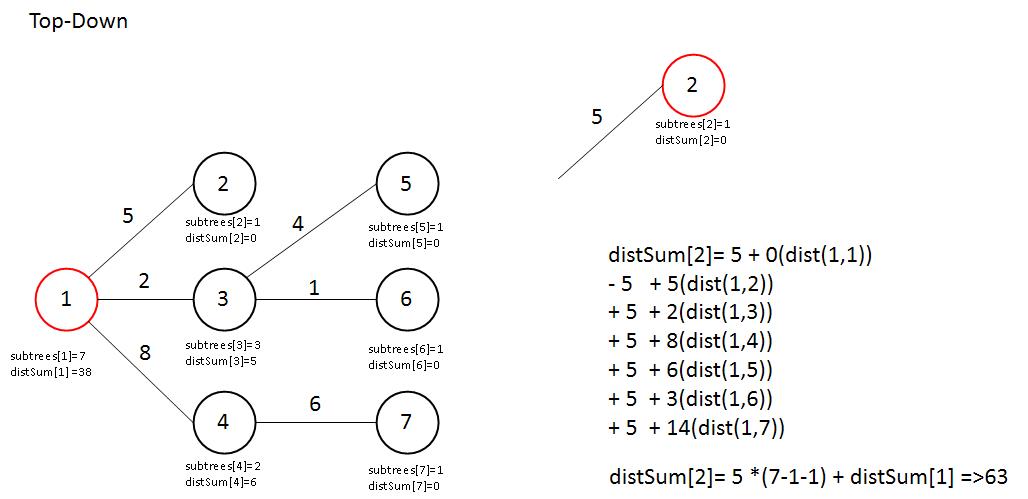
distSum[2]=weight(1,2)*(n-subtrees[2]-subtrees[2]) + distSum[1]

2번 노드에서 2번을 제외한 나머지 노드들을 가기 위해서는 (1,2) 간선을 지나게 된다. 또한, 간선을 지나가는 고려하여 각각의 노드에 대한 거리의 합을 구해보면 위와 같이 distSum[1] 즉 부모노드를 활용하여 거리합을 쉽게 도출 해낼 수 있다.

나머지에 대해서도 동일하게 수행하면 답을 도출할 수 있다.

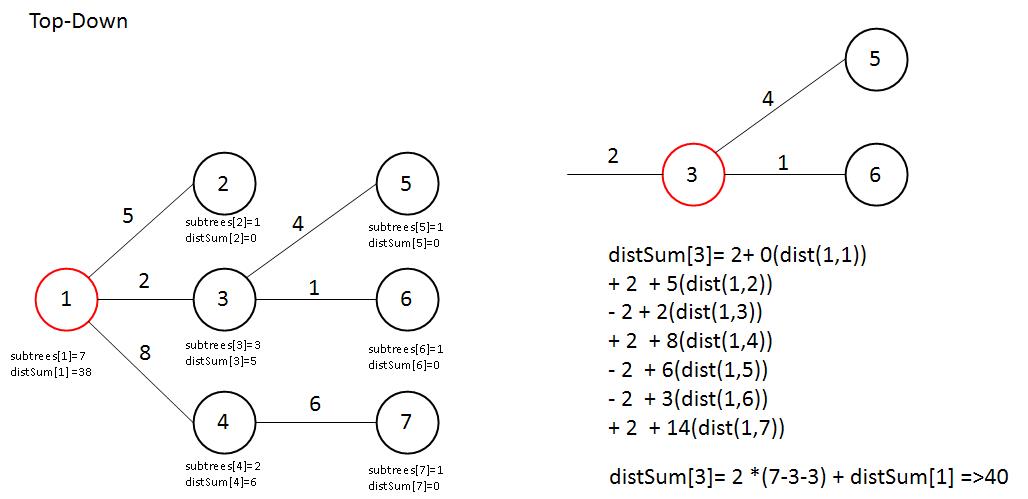
distSum[3]=weight(1,3)*(n-subtrees[3]-subtrees[3]) + distSum[1]

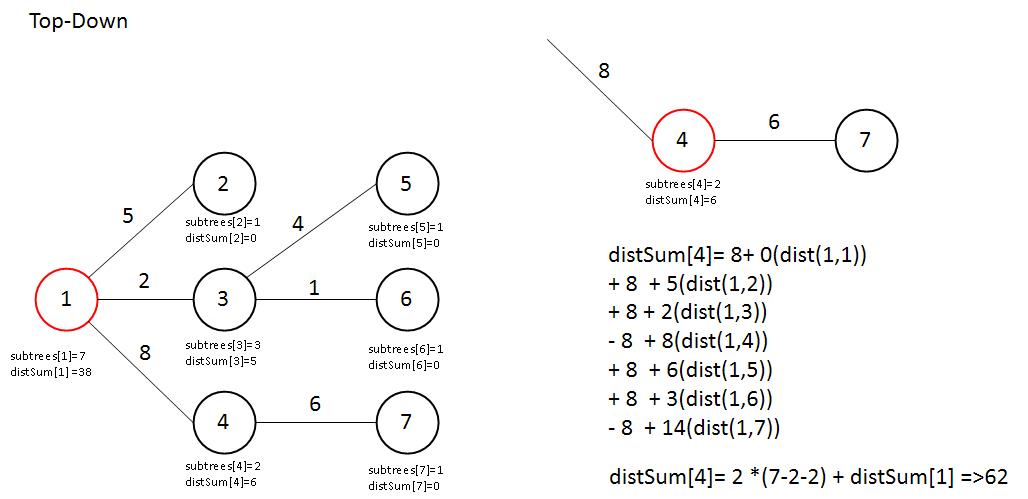
distSum[4]=weight(1,4)*(n-subtrees[4]-subtrees[4]) + distSum[1]

Solution

import sys

def dfs(vertex):
    global visited
    visited[vertex]=True
    subTrees[vertex]=1
    for adj_vertex,weight in graph[vertex]:
        if not visited[adj_vertex]:
            dfs(adj_vertex)
            distSum[vertex]+=distSum[adj_vertex] + subTrees[adj_vertex] * weight
            subTrees[vertex]+=subTrees[adj_vertex]
    return
       

def dfs_childs(vertex):
    global visited
    visited[vertex]=True
    for adj_vertex,weight in graph[vertex]:
        if not visited[adj_vertex]: 
            distSum[adj_vertex]=distSum[vertex]+(n_vertex-2*subTrees[adj_vertex])*weight
            dfs_childs(adj_vertex)
    return

if __name__ == "__main__":
    sys.setrecursionlimit(10**6)
    n_vertex=int(input())
    graph=[[] for _ in range(n_vertex+1)]

    for _ in range(n_vertex-1):
        v1,v2,weight=map(int,input().split())
        graph[v1].append((v2,weight))
        graph[v2].append((v1,weight))
    
    subTrees=[0] * (n_vertex+1)
    distSum=[0] *(n_vertex+1)
    
    visited=[False]*(n_vertex+1)
    dfs(1)
    visited=[False]*(n_vertex+1)
    dfs_childs(1)
    
    print("\n".join(map(str,distSum[1:])))