[BOJ] Q1219 오민식의 고민

[BOJ] Q1219 오민식의 고민

Question

Language: Python

Difficulty: Gold 1

상당히 까다로운 문제이다. 문제에 주어진 조건을 분석해보면 간선을 이용하게 되면 비용이 발생하고, 도시에 도착하면 보상금이 발생한다.

도착지에 도착할 수 없으면 ‘gg’ 돈을 무한히 벌 수 있으면 ‘gee’ 벌 수 있는 최대값

우선 무한히 많이 벌 수 있다? –> cycle이 존재한다는 의미이다. –> 우리가 흔히 최단거리 알고리즘 중에 사이클과 연관 있는 것은 bellman-ford 알고리즘이다.

그러면 음수 사이클의 조건에 맞게 가중치를 역전 시킨다, 즉 간선의 가중치는 양수로 만들고, 도시의 보상금은 음수로 만들게 된다. 이렇게 되면 도시에 도착하게 되면 간선의 가중치-도시의 보상금으로 되어서 음수 값이 된다는 의미는 그 도시를 도착하게 될때 수익이 발생한다는 의미로 해석할 수 있다. 그렇게 되면 음수 사이클이 발생한다면 돈을 무한히 많이 벌게 되는 것이다.

Fail Code 1

def solution():
    for i in range(v):
        for j in range(v):
            if graph[i][j] != inf:
                graph[i][j] -=city_earnings[j]
    
    for times in range(v):
        for i in range(v):
            for j in range(v):
                if graph[i][j] != inf:

                    if distance[j] > distance[i]+graph[i][j]:
                        distance[j]=distance[i]+graph[i][j]

                        if times==v-1:
                            return False
    
    return True

처음에는 이렇게 음수 사이클이 존재하기만 하면 무조건 돈을 무한히 벌 수 있다고 생각했다.

하지만 아래의 그림과 같은 경우가 있다면?

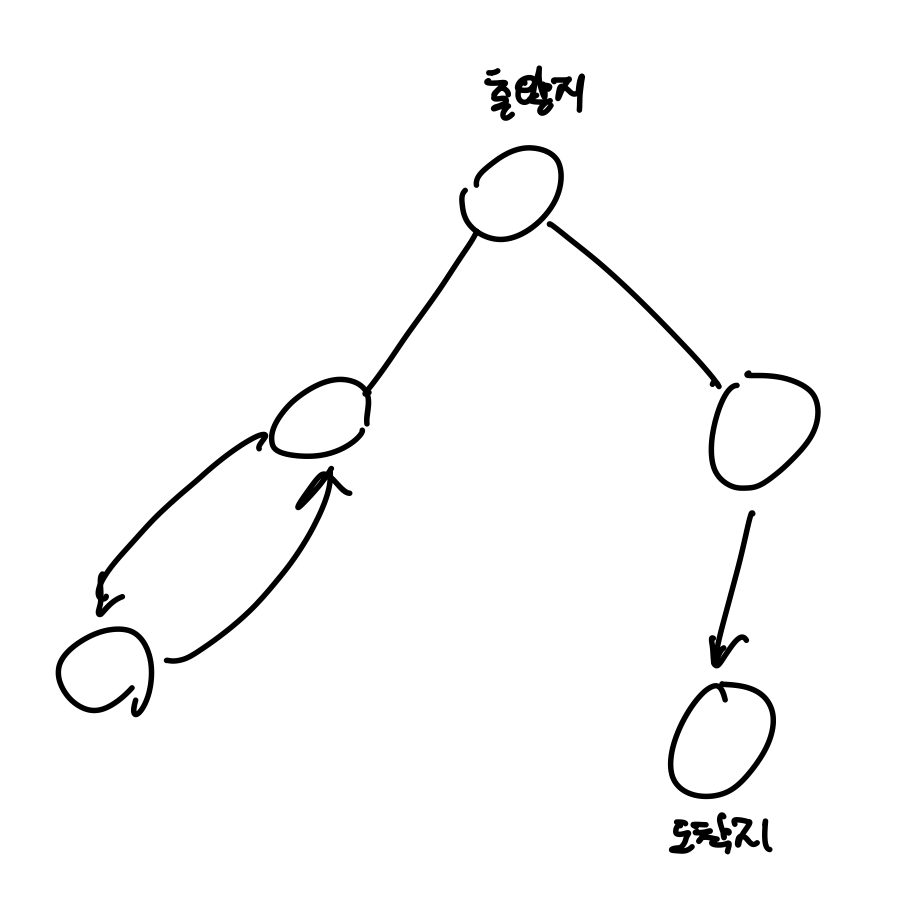
음수 사이클을 판단하는 것도 중요하지만, 사이클 내 도착지 노드가 존재하는 지를 확인해야된다.

Solution

from math import inf
from collections import deque

def solution():
    distances=[inf] *(v)
    distances[start]=-city_earnings[start]

    for i in range(e):
        edges[i][2]-=city_earnings[edges[i][1]]

    cycle=False
    reachable=False
    for times in range(v):
        for v1,v2,cost in edges:
            cost=distances[v1]+cost
            if distances[v2] > cost:
                distances[v2]=cost
                if times==v-1:
                    cycle=True
                    queue=deque([v2])
                    visited=[False]*(v)
                    
                    while queue:
                        vertex=queue.popleft()
                        visited[vertex]=True
                        
                        if vertex==end:
                            reachable=True
                        
                        for adj_vertex in graph[vertex]:
                            if not visited[adj_vertex]:
                                queue.append(adj_vertex)
    
    if distances[end]==inf:
        print("gg")
    else:
        if cycle and reachable:
            print("Gee")
        else:
            print(-distances[end])

if __name__ == "__main__":
v,start,end,e=map(int,input().split())
graph=[[] for _ in range(v)]
edges=[]
for _ in range(e):
        v1,v2,weight=map(int,input().split())
        graph[v1].append(v2)
        edges.append([v1,v2,weight])
city_earnings=list(map(int,input().split()))
solution()

그래서 위의 코드 처럼 bellman-ford 알고리즘을 통해 distances 배열을 최신화 시키고, 사이클이 생겼을 때는 bfs을 통해 도착지 노드가 사이클에 포함되어 있는지를 확인한다.