[Programmers] P150367 표현 가능한 이진트리

[Programmers] P150367 표현 가능한 이진트리

Question

Language: Python

해당 문제는 트리의 특성을 이용하여 루트 노드에서부터 자식 노드에 도달할 때까지 트리의 성립 여부를 검증하는 문제이다.

해당 문제를 풀이하기 위해 크게 2가지 과정이 필요하다

1. 십진수 -> 포화 이진 트리의 갯수에 맞는 이진수 변화
2. 해당 이진수에 맞는 트리 성립 여부

십진수 -> 이진수 변환

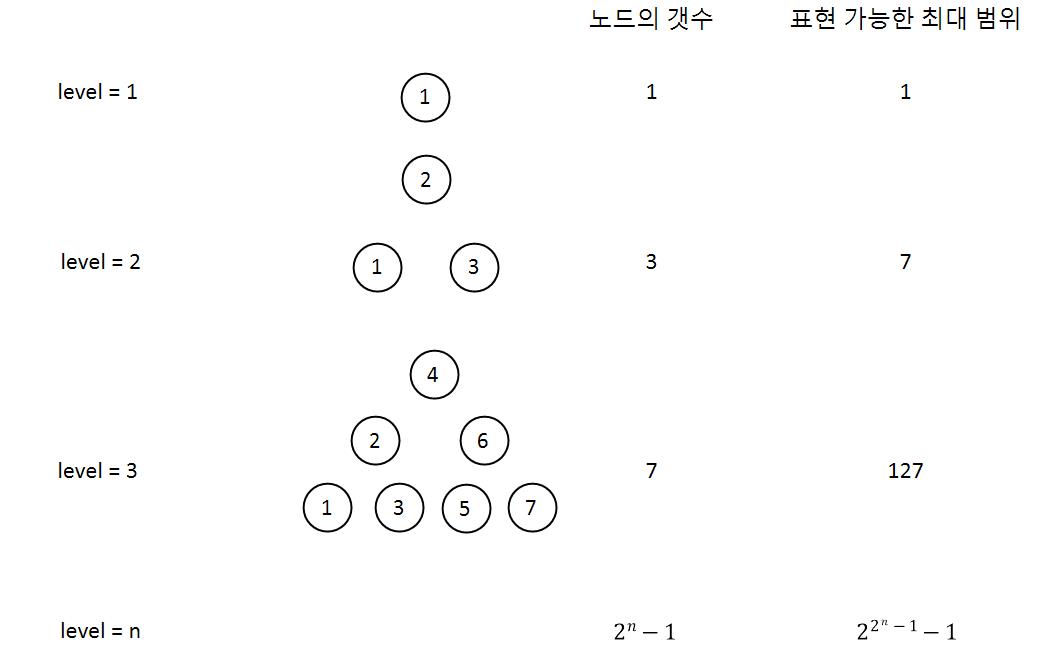
포화 이진트리의 경우 아래와 같은 규칙성을 가지게 되며, 이에 따라 십진수를 표현하기 위해 포화이진트리의 종류를 찾아낸다.

def find_full_length(number):
    depth=0
    for i in range(1,9):
        if number <=2**(2**i-1) -1:
            break
        depth=i
    return 2**(depth+1)-1

def solution():
    #포화 이진트리의 노드 갯수
    full_length=find_full_length(number)
    #루트 노드 번호
    root_number=(full_length+1)//2
    #기존의 십진수를 포화 이진트리 형태의 이진수로 변환
    tree_nodes=bin(number)[2:].zfill(full_length)

이진트리 성립 여부 확인

포화 이진트리의 특성상 왼쪽 서브트리와 오른쪽 서브 트리로 정확하게 양분하기 때문에 이러한 성질을 활용하여 아래의 그림과 같이 반복문을 수행하는 것이 가능하다.

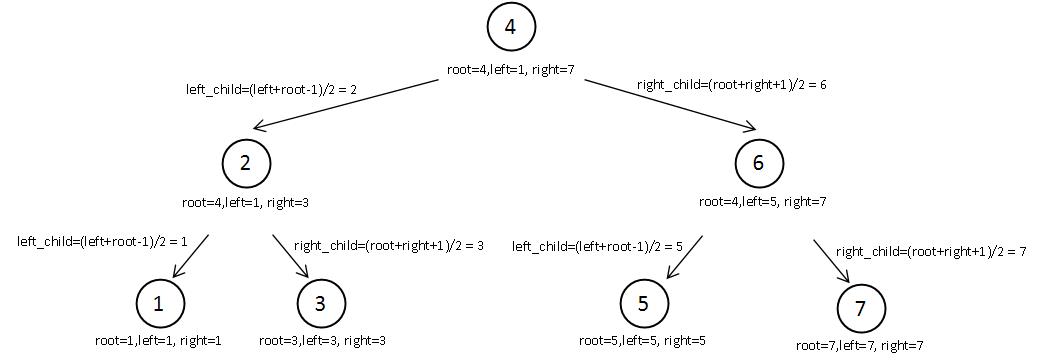
부모 노드에 대해서, 자식노드를 검증할 때, 부모 노드가 존재하지 않는데, 자식 노드가 존재하는 경우는 있을 수 없기 때문에 이러한 경우 트리가 성립할 수 없다라고 반환한다.

queue=deque([(root_number,1,full_length)])
    
    while queue:
        root,left,right=queue.popleft()
        
        #리프 노드 인 경우 더 이상 검사를 진행하지 않는다.
        if left==right:
            continue

        #부모 노드를 기준으로 왼쪽 자식과 오른쪽 자식 노드 번호값
        left_child=(left+root-1)//2
        right_child=(root+right+1)//2
        
        #왼쪽 자식 점검
        #부모 노드 없는데 왼쪽 자식 있는 경우는 있을 수 없다.
        if tree_nodes[root-1]=="0" and tree_nodes[left_child-1]=="1":
            return False
        queue.append((left_child,left,root-1))

        #부모 노드 없는데 오른쪽 자식 있는 경우는 있을 수 없다.
        if tree_nodes[root-1]=="0" and tree_nodes[right_child-1]=="1":
            return False
        queue.append((right_child,root+1,right))

    return True

Solution

from collections import deque
def find_full_length(number):
    depth=0
    for i in range(1,9):
        if number <=2**(2**i-1) -1:
            break
        depth=i
    return 2**(depth+1)-1

def check_if_available(number):
    full_length=find_full_length(number)

    root_number=(full_length+1)//2
    
    tree_nodes=bin(number)[2:].zfill(full_length)
    
    queue=deque([(root_number,1,full_length)])
    
    while queue:
        root,left,right=queue.popleft()
        
        if left==right:
            continue
        
        left_child=(left+root-1)//2
        right_child=(root+right+1)//2
        
        #왼쪽 자식 점검
        #부모 노드 없는데 왼쪽 자식 있는 경우는 있을 수 없다.
        if tree_nodes[root-1]=="0" and tree_nodes[left_child-1]=="1":
            return False
        queue.append((left_child,left,root-1))

        #부모 노드 없는데 오른쪽 자식 있는 경우는 있을 수 없다.
        if tree_nodes[root-1]=="0" and tree_nodes[right_child-1]=="1":
            return False
        queue.append((right_child,root+1,right))

    return True

def solution(numbers):
    answer = []
    for number in numbers:

        if check_if_available(number):
            answer.append(1)
        else:
            answer.append(0)
            
        
    return answer