[BOJ] Q1837 암호제작

[BOJ] Q1837 암호제작

Question

Language: Python

Difficulty: Bronze 3

해당 문제 자체는 소수 활용하여 모든 경우의 수를 고려하면 되는 비교적 간단한 문제이다. 소수를 구하기 위해 에라토스테네스의 체를 활용하면 된다.

Solution

from math import sqrt
def era_filter(k):
    checked=[True]*(k)
    primes=[]
    for number in range(2,k):
        if checked[number] == False:
            continue
        primes.append(number)
        times=2
        while number * times < k:
            checked[number*times]=False
            times+=1  
    return primes
    
def solution():
    primes=era_filter(k)
    
    for prime in primes:
        if secret % prime==0:
            print(f"BAD {prime}")
            break
    else:
        print("GOOD")

if __name__ == "__main__":
    secret,k=map(int,input().split())
    solution()

하지만, 이번 문제의 핵심은 P의 범위가 최대 10¹⁰⁰이라는 부분에 있다. 그렇기 때문에 나눗셈 연산 과정에서 overflow가 발생할 우려가 있다. 따라서, 이런 경우 숫자를 쪼개서 나눗셈을 진행하는 방안을 고려해야한다.

big number division

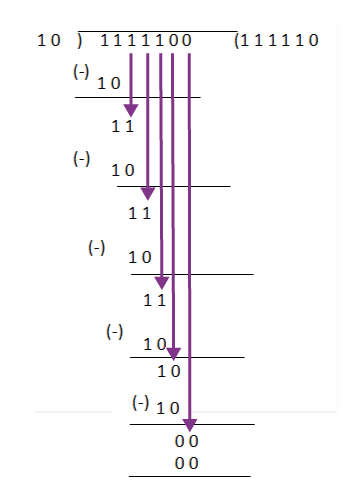
Bit-Division의 원리에서 착안것으로, 실제 나눗셈 과정을 로직화 하였다고 생각하면 이해하기 편할 것이다.

def perform_division(divisor):

    remainder=secret[0]
    quotient=0
    
    for index in range(1,length_of_secret+1):
        quotient=quotient * 10 + remainder//divisor
        remainder= remainder%divisor * 10 + secret[index]

    remainder= remainder%divisor
    return remainder,quotient

python buffer overflow

파이썬 외의 다른 언어의 경우 위와 같이 큰 숫자에 대해 쪼개서 연산을 진행하는 방향으로 구현해야 bit overflow가 발생하지 않는다. 하지만, python의 경우 자체적으로 유동적인 저장방식을 활용하여 overflow가 발생하지 않도록 한다.

파이썬_정수_오버플로우 에서 나온 부분을 참고 해보면 파이썬에서는 큰 숫자를 아래와 같은 방식으로 표현한다.

// 정수 타입을 나타내는 클래스(struct)
struct _longobject {
	PyObject_VAR_HEAD
	digit ob_digit[1];
};

위와 같은 배열 형태로 표현하면서 각각의 원소 단위로 분할해서 마치 비트 연산을 수행하는 것처럼 각종 사칙연산에 대해 오버플로우 걱정 없이 수행할 수 있게 된다.