[BOJ] Q14500 테트로미노
[BOJ] Q14500 테트로미노
Question
Language: Python
Difficulty: Gold 4
해당 문제는 2가지 풀이를 고려해서 풀이하는 것이 가능하다.
- 모든 도형에 대한 고려 각각의 도형을 원점을 기준으로 좌표를 표현해서 모든 좌표에 대해 해당 테트로미노를 넣을 수 있는 지 판단하고, 해당 테트로미노가 놓여있는 자리의 값을 확인해서 최댑값을 갱신한다.
shapes_group=[[] for _ in range(5)]
shapes_group[0]=[[(0,0),(0,1),(0,2),(0,3)],[(0,0),(1,0),(2,0),(3,0)]] # 1번 모양
shapes_group[1]=[[(0,0),(0,1),(1,0),(1,1)]] #2번 모양
shapes_group[2]=[[(0,0),(1,0),(2,0),(2,1)],[(0,0),(0,1),(0,2),(1,0)],[(0,1),(1,1),(2,0),(2,1)],[(0,0),(1,0),(1,1),(1,2)],[(0,2),(1,0),(1,1),(1,2)],[(0,0),(0,1),(1,1),(2,1)],[(0,0),(0,1),(0,2),(1,2)],[(0,0),(0,1),(1,0),(2,0)]] # 3번 모양
shapes_group[3]=[[(0,0),(1,0),(1,1),(2,1)],[(0,1),(0,2),(1,0),(1,1)],[(0,0),(0,1),(1,1),(1,2)],[(0,1),(1,0),(1,1),(2,0)]] # 4번 모양
shapes_group[4]=[[(0,0),(0,1),(0,2),(1,1)],[(0,1),(1,0),(1,1),(2,1)],[(0,1),(1,0),(1,1),(1,2)],[(0,0),(1,0),(1,1),(2,0)]]# 5번 모양
- dfs를 이용한 도형 추적 테트로미노는 4개의 정사각형을 이어 붙여 만들 수 있는 도형의 종류로 이는 특정 한 지점에서 거리가 4가 되는 좌표점들의 경로와 똑같은 모형을 보인다.
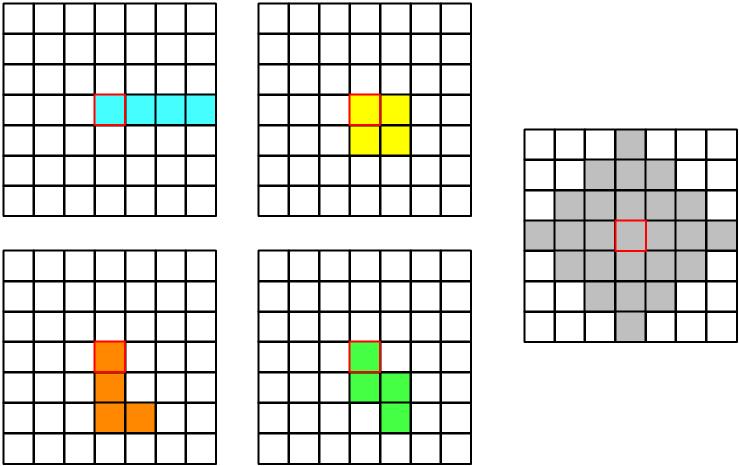
한번에 연결할 수 없는(한붓그리기가 안되는, 연속된 선으로 이을 수 없는) 경우는 따로 위의 방식처럼 좌표로 표현해서 처리한다.
tetrominos=[[(0,1),(1,0),(1,1),(1,2)],[(0,0),(0,1),(0,2),(1,1)],[(0,0),(1,0),(2,0),(1,1)],[(1,0),(0,1),(1,1),(2,1)]]
Solution 1
def if_possible_count_score(shape,row,col):
count=0
for dy,dx in shape:
next_row=row+dy
next_col=col+dx
#경계를 넘어서는 경우
if next_row < 0 or next_row >=n_rows or next_col < 0 or next_col >= n_cols:
return False
count+=graph[next_row][next_col]
return count
def solution():
shapes_group=[[] for _ in range(5)]
shapes_group[0]=[[(0,0),(0,1),(0,2),(0,3)],[(0,0),(1,0),(2,0),(3,0)]] # 1번 모양
shapes_group[1]=[[(0,0),(0,1),(1,0),(1,1)]] #2번 모양
shapes_group[2]=[[(0,0),(1,0),(2,0),(2,1)],[(0,0),(0,1),(0,2),(1,0)],[(0,1),(1,1),(2,0),(2,1)],[(0,0),(1,0),(1,1),(1,2)],[(0,2),(1,0),(1,1),(1,2)],[(0,0),(0,1),(1,1),(2,1)],[(0,0),(0,1),(0,2),(1,2)],[(0,0),(0,1),(1,0),(2,0)]] # 3번 모양
shapes_group[3]=[[(0,0),(1,0),(1,1),(2,1)],[(0,1),(0,2),(1,0),(1,1)],[(0,0),(0,1),(1,1),(1,2)],[(0,1),(1,0),(1,1),(2,0)]] # 4번 모양
shapes_group[4]=[[(0,0),(0,1),(0,2),(1,1)],[(0,1),(1,0),(1,1),(2,1)],[(0,1),(1,0),(1,1),(1,2)],[(0,0),(1,0),(1,1),(2,0)]]# 5번 모양
max_count=0
for start_row in range(n_rows):
for start_col in range(n_cols):
for shapes in shapes_group:
for shape in shapes:
result=if_possible_count_score(shape,start_row,start_col)
if result == False:
continue
else:
max_count=max(max_count,result)
return max_count
if __name__ == "__main__":
n_rows,n_cols=map(int,input().split())
graph=[list(map(int,input().split())) for _ in range(n_rows)]
print(solution())
Solution 2
import os
from collections import deque
#테트로미노는 길이가 4인 dfs으로 해결 가능하다
def dfs(index,row,col,sum):
global max_sum,visited
if index==4:
max_sum=max(max_sum,sum)
return
for dir in range(4):
next_row=row+dy[dir]
next_col=col+dx[dir]
if next_row < 0 or next_row>=n_rows or next_col < 0 or next_col>=n_cols:
continue
if visited[next_row][next_col]:
continue
visited[next_row][next_col]=True
dfs(index+1,next_row,next_col,sum+board[next_row][next_col])
visited[next_row][next_col]=False
#하지만 분홍색 모형은 dfs으로 풀이가 불가능하다, 그래서 따로 처리해준다. ㅗ,ㅜ,ㅏ,ㅓ
def check_tetromino(row,col):
global max_sum
tetrominos=[[(0,1),(1,0),(1,1),(1,2)],[(0,0),(0,1),(0,2),(1,1)],[(0,0),(1,0),(2,0),(1,1)],[(1,0),(0,1),(1,1),(2,1)]]
for tetromino in tetrominos:
sum=0
for dy,dx in tetromino:
next_row=row+dy
next_col=col+dx
if next_row < 0 or next_row>=n_rows or next_col<0 or next_col>=n_cols:
break
sum+=board[next_row][next_col]
else:
max_sum=max(max_sum,sum)
def solution():
for row in range(n_rows):
for col in range(n_cols):
dfs(0,row,col,0)
check_tetromino(row,col)
def solution():
for row in range(n_rows):
for col in range(n_cols):
dfs(0,row,col,0)
check_tetromino(row,col)
if __name__ == "__main__":
#predefined globals
n_rows,n_cols=map(int,input().split())
board=[list(map(int,input().split())) for _ in range(n_rows)]
#other globals
max_sum=0
dy=[-1,0,1,0]
dx=[0,1,0,-1]
visited=[[False] * n_cols for _ in range(n_rows)]
solution()
print(max_sum)

댓글남기기