[BOJ] Q14476 최대공약수 하나 빼기

[BOJ] Q14476 최대공약수 하나 빼기

Question

Language: Python

Difficulty: Gold 2

해당 문제의 경우, 누적합과 같이 특정 구간에 대한 합을 저장하는 방식처럼 특정 구간에 대한 최대공약수를 저장한 배열을 구해서 문제 풀이에 적용할 수 있다.

누적 최대공약수

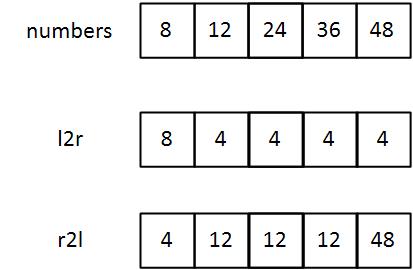
#왼쪽에서 오른쪽으로의 누적 최대공약수
for i in range(1,n):
    l2r[i]=gcd(l2r[i-1],numbers[i])

#오른쪽에서 왼쪽으로의 누적 최대공약수
for i in range(n-2,-1,-1):
    r2l[i]=gcd(r2l[i+1],numbers[i])

최대공약수에 대해서는 결합법칙이 성립하기 때문에, 누적합과 같이 특정 구간에 대한 i번째 전까지의 수들에 대한 최대공약수를 저장할 수 있다.

i 번째 숫자를 제외한 나머지 수들에 대한 최대공약수 구하기

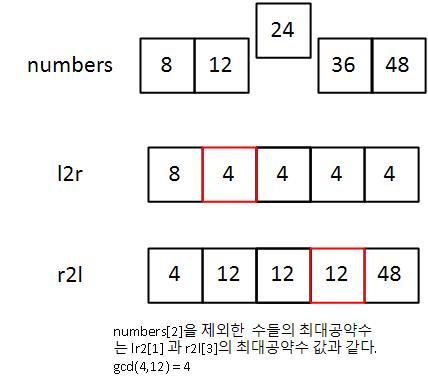
#첫번째 값을 빼는 경우
if i==0:
    max_gcd=r2l[1]
#마지막 값을 빼는 경우
elif i==n-1:
    max_gcd=l2r[n-2]
#그 외의 경우
else:
    max_gcd=gcd(l2r[i-1],r2l[i+1])

그래서, 왼쪽에서 오른쪽으로의 누적 최대공약수, 오른쪽에서 왼쪽으로의 누적 최대공약수를 미리 구해놓게 되면 i 번째 숫자를 제외한 나머지 숫자들에 최대 공약수를 쉽게 구할 수 있다.

Solution

from math import gcd

def solution():
    l2r=[numbers[0]]*n
    r2l=[numbers[n-1]]*n

    #왼쪽에서 오른쪽으로의 누적 최대공약수
    for i in range(1,n):
        l2r[i]=gcd(l2r[i-1],numbers[i])
    
    #오른쪽에서 왼쪽으로의 누적 최대공약수
    for i in range(n-2,-1,-1):
        r2l[i]=gcd(r2l[i+1],numbers[i])
    

    answer=[]

    for i in range(n):
        #첫번째 값을 빼는 경우
        if i==0:
            max_gcd=r2l[1]
        #마지막 값을 빼는 경우
        elif i==n-1:
            max_gcd=l2r[n-2]
        #그 외의 경우
        else:
            max_gcd=gcd(l2r[i-1],r2l[i+1])
        #만약 구한 최대공약수가 제거한 숫자의 약수인 경우 --> 문제의 조건에 부합하지 않음
        if numbers[i] % max_gcd !=0:
            answer.append((max_gcd,numbers[i]))

    answer.sort(key=lambda x: -x[0])
    print(" ".join(map(str,answer[0])) if answer else -1)

if __name__ == "__main__":
    n=int(input())
    numbers=list(map(int,input().split()))
    solution()