[BOJ] Q2637 장난감 조립

[BOJ] Q2637 장난감 조립

Question

Language: Python

Difficulty: Gold 2

해당 문제는 topological sorting을 이용해서 장남감 간에 의존성을 토대로 중간 블록에서 요구되는 기본 블록 수를 계산해 나가야 한다.

중간 블록 별로 기본 블록수를 저장하기 위한 이차원 배열을 생성한다.

각 행(중간블록) 별로 필요한 기본블록 정보를 열에 나타낸다.

	1	2	3	4	5	6	7
1	0	0	0	0	0	0	0
2	0	0	0	0	0	0	0
3	0	0	0	0	0	0	0
4	0	0	0	0	0	0	0
5	0	0	0	0	0	0	0
6	0	0	0	0	0	0	0
7	0	0	0	0	0	0	0

그래프 생성

중간 블록을 만들어 내기 위해 기본 블록이 필요하다는 것은 기본 블록에서 중간블록으로 향하는 의존관계가 있다는 말이다. 그래서 해당 의존관계를 그래프로 표현하면 아래와 같다.

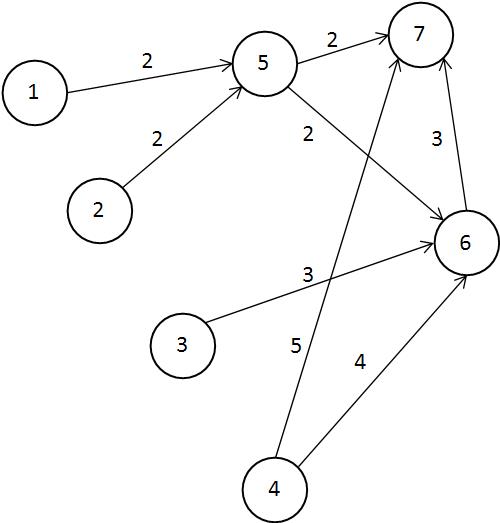
그리고 해당 그래프에 대한 topological sorting을 진행하면 1,2,3,4,5,6,7 와 같다

순차적으로 순회를 하면서 각각의 중간 블록에 대한 정보를 누적시켜준다.

Topological Sorting

기본 블록에 대한 순회

기본 블록 1번은 중간 블록 5번에 연결되어 있다, 그리고 5번 블록을 표현하기 위해 1번 블록이 2개 필요하므로 아래와 같이 2를 늘려준다.

	1	2	3	4	5	6	7
1	0	0	0	0	0	0	0
2	0	0	0	0	0	0	0
3	0	0	0	0	0	0	0
4	0	0	0	0	0	0	0
5	2	0	0	0	0	0	0
6	0	0	0	0	0	0	0
7	0	0	0	0	0	0	0

위에 대한 알고리즘은 아래와 같다.

if vertex in basic_block_types:
    block_map[adj_vertex][vertex]+=cost

다음 순서인 2번을 순회하면 아래와 같아진다.

	1	2	3	4	5	6	7
1	0	0	0	0	0	0	0
2	0	0	0	0	0	0	0
3	0	0	0	0	0	0	0
4	0	0	0	0	0	0	0
5	2	2	0	0	0	0	0
6	0	0	0	0	0	0	0
7	0	0	0	0	0	0	0

3,4을 순회 하면 아래와 같아진다.

	1	2	3	4	5	6	7
1	0	0	0	0	0	0	0
2	0	0	0	0	0	0	0
3	0	0	0	0	0	0	0
4	0	0	0	0	0	0	0
5	2	2	0	0	0	0	0
6	0	0	3	4	0	0	0
7	0	0		5	0	0	0

중간 블록 순회

이제 중간 블록인 5번이 순회된다

중간 블록의 경우 다른 중간 블록을 만들기 위해 해당 중간 블록을 만들기 위한 모든 기본블록이 모두 쓰인다. 중간 블록 A를 만들기 위해 중간 블록 B가 2개 필요하다면, 중간 블록 A를 만들기 위해서는 중간 블록 B를 구성하는 모든 기본 블록에 대해 각각 2개씩 필요하게 되는 것이다.

	1	2	3	4	5	6	7
1	0	0	0	0	0	0	0
2	0	0	0	0	0	0	0
3	0	0	0	0	0	0	0
4	0	0	0	0	0	0	0
5	2	2	0	0	0	0	0
6	4	4	3	4	0	0	0
7	4	4		5	0	0	0

위의 작업에 대한 알고리즘은 아래와 같다.

for block in basic_block_types:
    block_map[adj_vertex][block]+=(cost*block_map[vertex][block])

최종적으로 7번을 순회하면 아래와 같다

	1	2	3	4	5	6	7
1	0	0	0	0	0	0	0
2	0	0	0	0	0	0	0
3	0	0	0	0	0	0	0
4	0	0	0	0	0	0	0
5	2	2	0	0	0	0	0
6	4	4	3	4	0	0	0
7	16	16	9	17	0	0	0

Solution

from collections import deque
def solution():
    basic_block_types=list(set([i for i in range(1,n_blocks+1)])-set(mid_block_types))

    basic_block_types.sort()
    mid_block_types.sort()   

    block_map=[[0] *(n_blocks+1) for i in range(n_blocks+1)]


    queue=deque()

    for i in range(1,n_blocks+1):
        if indegree[i]==0:
            queue.append(i)
    
    while queue:
        vertex=queue.popleft()

        for adj_vertex,cost in graph[vertex]:
            indegree[adj_vertex]-=1
            if vertex in basic_block_types:
                block_map[adj_vertex][vertex]+=cost
            else:
                for block in basic_block_types:
                    block_map[adj_vertex][block]+=(cost*block_map[vertex][block])

            if indegree[adj_vertex]==0:
                queue.append(adj_vertex)

    for basic_block in basic_block_types:
        print(basic_block,block_map[n_blocks][basic_block])

if __name__ == "__main__":
    mid_block_types=[]
    n_blocks=int(input())
    indegree=[0 for _ in range(n_blocks+1)]
    graph=[[] for _ in range(n_blocks+1)]
    n_relations=int(input())
    for _ in range(n_relations):
        end,start,counts=list(map(int,input().split()))
        indegree[end]+=1
        graph[start].append((end,counts))
        mid_block_types.append(end)

    solution()