[BOJ] Q1005 ACM Craft

[BOJ] Q1005 ACM Craft

Question

Language: Python

Difficulty: Gold 3

우선 특정 건물을 짓는데 특정 건물이 지어진 뒤 지어질 수 있다. –> 건물간에 의존관계가 존재한다 –> Topological Sorting을 수행해야한다.

아래와 같이 건물간의 의존성 관계를 표현한 그래프가 있다고 하자

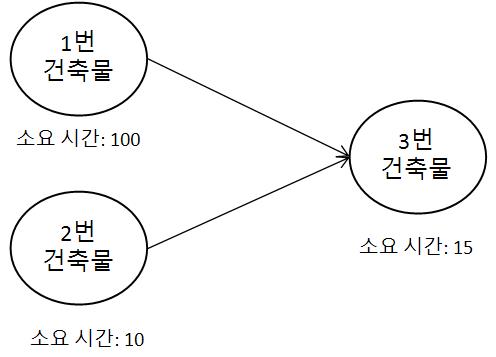
건물 3번을 짓기 위해서는 건물 1과 건물 2가 지어져야한다. 건물 1, 2는 동시에 짓는 것을 시작할 수 있다.

하지만, 건물 1번이 지어지기 전까지는 3번 건물을 지을 수 없다. 이 처럼 의존성을 가진 건물에 대해서 선수 관계에 있는 건물 중에 건축 시간이 가장 긴 값을 기준으로 건물을 건축을 시작할 수 있다.

아래의 Topological Sorting 과정을 살펴보자

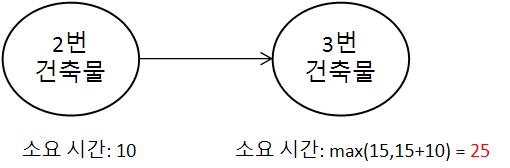우선 건물 2가 지어진 후, 건물 3을 짓게 되면 건물 3에 대한 건축 시간은 25이다

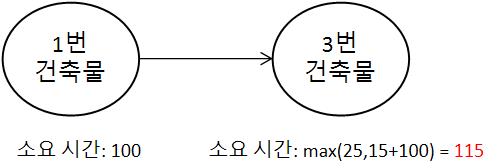하지만, 건물 1또한 건물 3에 대한 의존 관계를 가지고 있고, 건축 기간을 살펴 봤을때, 건물 1에대한 건축 시간이 더 많이 소요되므로, 건축 1에대한 건축 시간을 기준으로 건물 3번의 건축 시간을 잡아야한다.

Solution

from collections import deque
from copy import deepcopy

def solution():
    time_passed=0
    #각 건물의 건축 완료 시간은 처음에는 각 건물에 대한 건축 시간으로 초기화한다.
    distance=deepcopy(weight)
    queue=deque()
    for i in range(1,n_vertex+1):
        if indegree[i]==0:
            queue.append(i)

    while queue:
        vertex= queue.popleft()

        if vertex == target:
            break
        for adj_vertex in graph[vertex]:
            indegree[adj_vertex]-=1
            #선수 관계의 건물에 대해서 가장 긴 건출 시간을 가지는 건축 시간으로 기준으로 현재 건물의 건축시간을 잡는다.
            distance[adj_vertex-1]=max(distance[adj_vertex-1],distance[vertex-1]+weight[adj_vertex-1])

            if indegree[adj_vertex]==0:
                queue.append(adj_vertex)
        #만약, target 건물이 indegree=0 즉, 지을 수 있으면 topological sorting을 멈춘다.
        if target in queue:
            break
                
             
    return distance[target-1]

if __name__ == "__main__":
    test_cases=int(input())
    for _ in range(test_cases):
        n_vertex,n_rules=map(int,input().split())
        weight=list(map(int,input().split()))
        graph=[[] for _ in range(n_vertex+1)]
        indegree=[0] * (n_vertex+1)
        for _ in range(n_rules):
            start,end=map(int,input().split())
            graph[start].append(end)
            indegree[end]+=1
        
        target=int(input())
        print(solution())