[BOJ] Q2042 구간 합 구하기

[BOJ] Q2042 구간 합 구하기

Question

Language: Python

Difficulty: Gold 1

해당 문제는 segment tree를 활용하는 대표적인 문제이다.

Solution

from collections import defaultdict
from bisect import bisect_right

def init(index,start,end):
    global tree
    #리프 노드에 다달한 경우
    if start==end:
        tree[index]=numbers[start-1]
        return tree[index]
    
    mid=(start+end)//2

    tree[index]=init(index*2,start,mid)+init(index*2+1,mid+1,end)
    return tree[index]

def sum_of_interval(index,start,end,left,right):
    #범위를 벗어나는 경우
    if right < start or end < left:
        return 0
    #범위 안에 있는 경우
    if left<=start and end <=right:
        return tree[index]
    #범위가 걸쳐있는 경우
    mid=(start+end)//2
    return sum_of_interval(index*2,start,mid,left,right)+sum_of_interval(index*2+1,mid+1,end,left,right)

def update_value(index,start,end,change_index,diff):
    #범위 밖에 있는 경우
    if change_index < start or end < change_index:
        return
    tree[index]+=diff
    
    #리프 노드에 도달한 경우
    if start==end:
        return

    mid=(start+end)//2

    update_value(index*2,start,mid,change_index,diff)
    update_value(index*2+1,mid+1,end,change_index,diff)
    

def solution():
    init(1,1,n)
   
    for a,b,c in commands:
        #수를 바꾸는 옵션
        if a==1:
            diff=(c-numbers[b-1])
            numbers[b-1]=c
            update_value(1,1,n,b,diff)
                 
        #구간합을 구하는 옵션
        else:
            print(sum_of_interval(1,1,n,b,c))


if __name__ == "__main__":
    n,m,k=map(int,input().split())
    numbers=[int(input()) for _ in range(n)]
    commands=[list(map(int,input().split())) for _ in range(m+k)]
    tree=[0]*(4*n)
    solution()

segment Tree

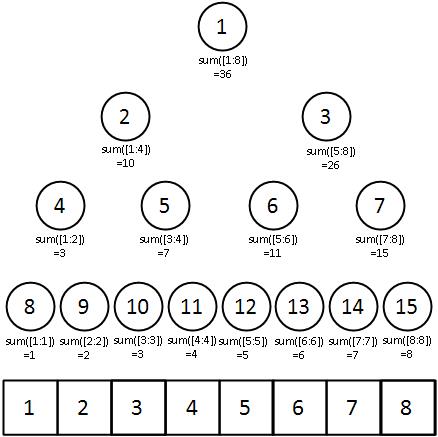
위의 그림과 같이 구간합에 대해서 저장하고 있는 트리의 형태를 segment tree라고 한다. 위와 같이 저장함으로써 필요한 구간합 혹은 특정 인덱스의 수정 이후의 구간합이 필요한 경우에 대해서 빠른 연산을 수행할 수 있다.

Tree 초기화

–> 각 노드 별로 구간에 따른 구간합을 구해준다.

def init(index,start,end):
    global tree
    #리프 노드에 다달한 경우
    if start==end:
        tree[index]=numbers[start-1]
        return tree[index]
    
    mid=(start+end)//2

    tree[index]=init(index*2,start,mid)+init(index*2+1,mid+1,end)
    return tree[index]

구간합 구하기

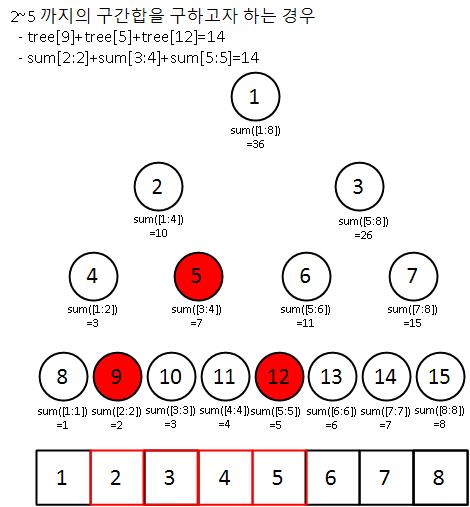
특정 구간에 대한 합을 구하고자 하는 경우 해당 구간을 포함하는 노드의 합을 통해 구간합을 구할 수 있다.

def sum_of_interval(index,start,end,left,right):
    #범위를 벗어나는 경우
    if right < start or end < left:
        return 0
    #범위 안에 있는 경우
    if left<=start and end <=right:
        return tree[index]
    #범위가 걸쳐있는 경우
    mid=(start+end)//2
    return sum_of_interval(index*2,start,mid,left,right)+sum_of_interval(index*2+1,mid+1,end,left,right)

값의 수정

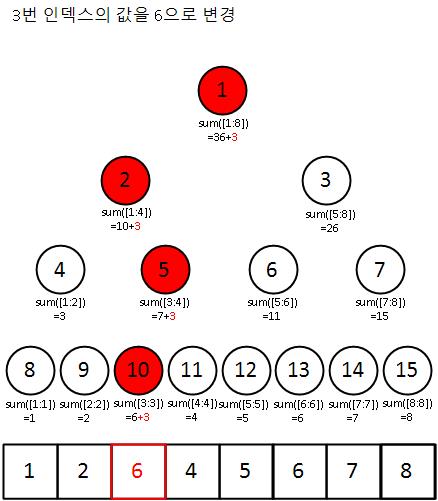
특정 값의 수정을 진행하기 위해, 해당 인덱스를 포함하는 구간합을 저장하고 있는 트리의 노드 값에 기존값에 대한 변화량 만큼을 더해준다.

def update_value(index,start,end,change_index,diff):
    #범위 밖에 있는 경우
    if change_index < start or end < change_index:
        return
    tree[index]+=diff
    
    #리프 노드에 도달한 경우
    if start==end:
        return

    mid=(start+end)//2

    update_value(index*2,start,mid,change_index,diff)
    update_value(index*2+1,mid+1,end,change_index,diff)

위와 같이 트리 형태로 범위에 따른 구간합들을 저장하므로써 구간합을 구하는 과정과 값을 수정하는 과정을 O(log(n))[n은 segment tree의 높이] 내에 해결하는 것이 가능하다. 분할 정복 + 트리가 활용된 자료구조의 형태이다.