Shortest Path

Shortest Path

최단경로 찾기 문제에서 가장 많이 사용되는 알고리즘은 크게 3가지가 있다.

Dijkstra Alogrithm

다이직스트라 알고리즘은 대표적인 SSSP(Single Source Shortest Path)문제를 해결하는 알고리즘이다. 하나의 시작 노드에 대해 다른 노드들에 도달하는 최소 거리를 구할 수 있다.

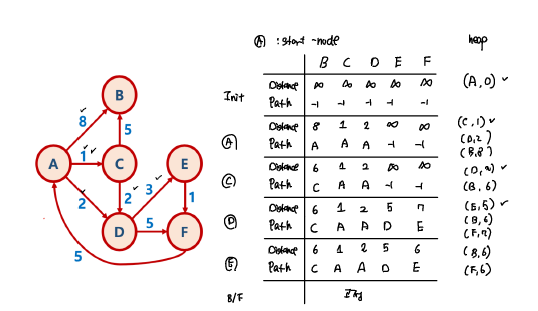
다이직스트라 알고리즘에서 핵심적인 부분은 해당 노드를 경유해서 가는 거리와 기존의 거리를 비교해서 만약 경유해서 갈 경우가 더 짧은 경우 해당 거리로 최신화 시켜준다. 매 반복마다 아래의 코드를 실행하면서 경로를 최소화 시킨다.

한 노드에서 거리 최신화를 완료하면은 방문하지 않은 노드 중에서 가장 가까운 노드를 선택해서 해당 작업을 반복해서 수행한다.

for adj_node,weight in graph[node]:
  if distance[adj_node] > distance[node] + weight:
    distance[adj_node] = distance[node] + weight:

Source

import math, heapq
def dijkstra_path(graph,n,start_vertex,end_vertex):
  distance=[math.inf] * (n+1)
  path=[-1] * (n+1)

  heap=[]
  heapq.heappush(heap,(0,start_vertex))
  distance[start_vertex]=0

  while heap:
    weight,vertex=heapq.heappop(heap)
    if distance[vertex] < weight:
      continue
    for adj_vertex,weight in graph[vertex]:
      temp=distance[vertex] + weight
      if distance[adj_vertex] > temp:
        distance[adj_vertex]=temp
        path[adj_vertex]=vertex
        heapq.heappush(heap,(temp,adj_vertex))

  return distance

Time Complexity

Heap를 이용해서 구현한 경우: O(ElogE) –>각 노드에 대한 거리값을 heap를 통해 관리하여 노드를 찾는 과정을 빨리한다.

그렇지 않은 경우: O(V²) –> 최소 거리에 있는 노드를 찾기 위해 매 노드를 모두 탐색해야하므로

Floyd-Warshall Algorithm

플로이드 워셜 알고리즘은 ASSP(All Souce Shortest Path)문제를 해결하기 위한 알고리즘이다. 해당 알고리즘의 핵심은 아래의 코드이다. 모든 노드에서 노드로부터 다른 특정 노드를 거쳤을 때 특정 노드를 경유해서 가는 경우가 짧을 때 짧은 거리로 최신화 시켜준다.

for k in range(n):
  for a in range(n):
    for b in range(n):
      if distance[a][b] > distance[a][k] + distance[k][b]:
        distance[a][b] = distance[a][k] + distance[k][b]:

Source

def floyd_warshall_path(graph,n):
  distance=[[math.inf] * (n+1) for _ in range(n+1)]

  for a in range(1,n+1):
    distance[a][a]=0

  for vertex in range(1,n+1):
    for adj_vertex,weight in graph[vertex]:
      distance[vertex][adj_vertex]=weight
        
  for k in range(1,n+1):
    for a in range(1,n+1):
      for b in range(1,n+1):
        distance[a][b]=min(distance[a][b],distance[a][k] + distance[k][b])
  
  return distance

Time Complexity: O(V³)

Bellman-Ford Algorithm

보통은 Dijkstra, Floyd-warshall 알고리즘으로 경로 찾기 문제를 해결할 수 있다 하지만, edge에 설정된 weight 값이 음수인 경우에는 위 2개의 알고리즘으로는 해결할 수 없다. 이때 사용하는 것이 Belman-ford 알고리즘이다.

모든 노드를 한번 씩 거쳐가면서 간선을 점검함으로써 해당 노드로의 거리값을 최신화 시키면 된다. 하지만, 모든 노드를 다 거쳐 간 이후에도 거리가 수정되는 경우가 발생하는 경우가 있는데 이는 음수 사이클이 발생한 것이다.

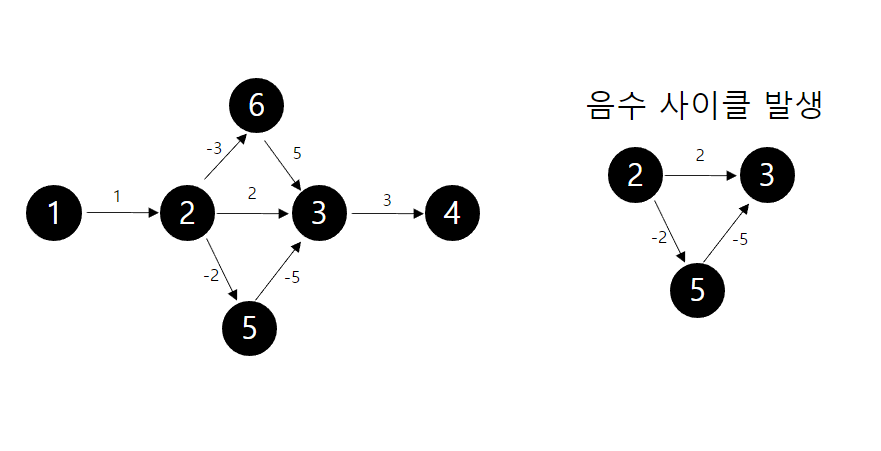
위와 같이 사이클 내 weight의 합이 음수인 경우 순환을 하면서 계속 거리가 음수방향으로 커지고 결국 음의 무한대로 작아지게 된다. 따라서 이러한 음수 사이클이 있을 때는 최단 경로를 구하는 것이 어렵다. 이러한 음수 사이클을 찾기 위해 아래의 코드에서 V번째 돌때 거리가 최신화 되었을 때의 조건문을 삽입한다.

Source

def bellman_ford(graph,n,start_vertex,end_vertex):
  distance=[math.inf] * (n+1)

  distance[start_vertex]=0
  
  for i in range(n):
    for vertex in range(1,n+1):
      for adj_vertex,weight in graph[vertex]:
        if distance[adj_vertex] > weight+ distance[vertex]:
          distance[adj_vertex] = weight+ distance[vertex]
          
          //v번째 거리가 최신화 되면 이는 음수 사이클이 존재함을 의미한다.
          if i==n-1:
            return False

  return distance

Question Types

최단 경로 찾는 문제는 보통 그래프 관련 문제와 같이 병행해서 나오는 빈출 유형으로 반드시 위에 3가지 알고리즘에 대해서는 명확한 이해가 요구된다.