Graph

Graph

그래프는 노드와 간선을 가지는 집합으로, 간선이 방향성을 가지는 방향 그래프가 있고, 방향이 없는 무방향 그래프가 있다.

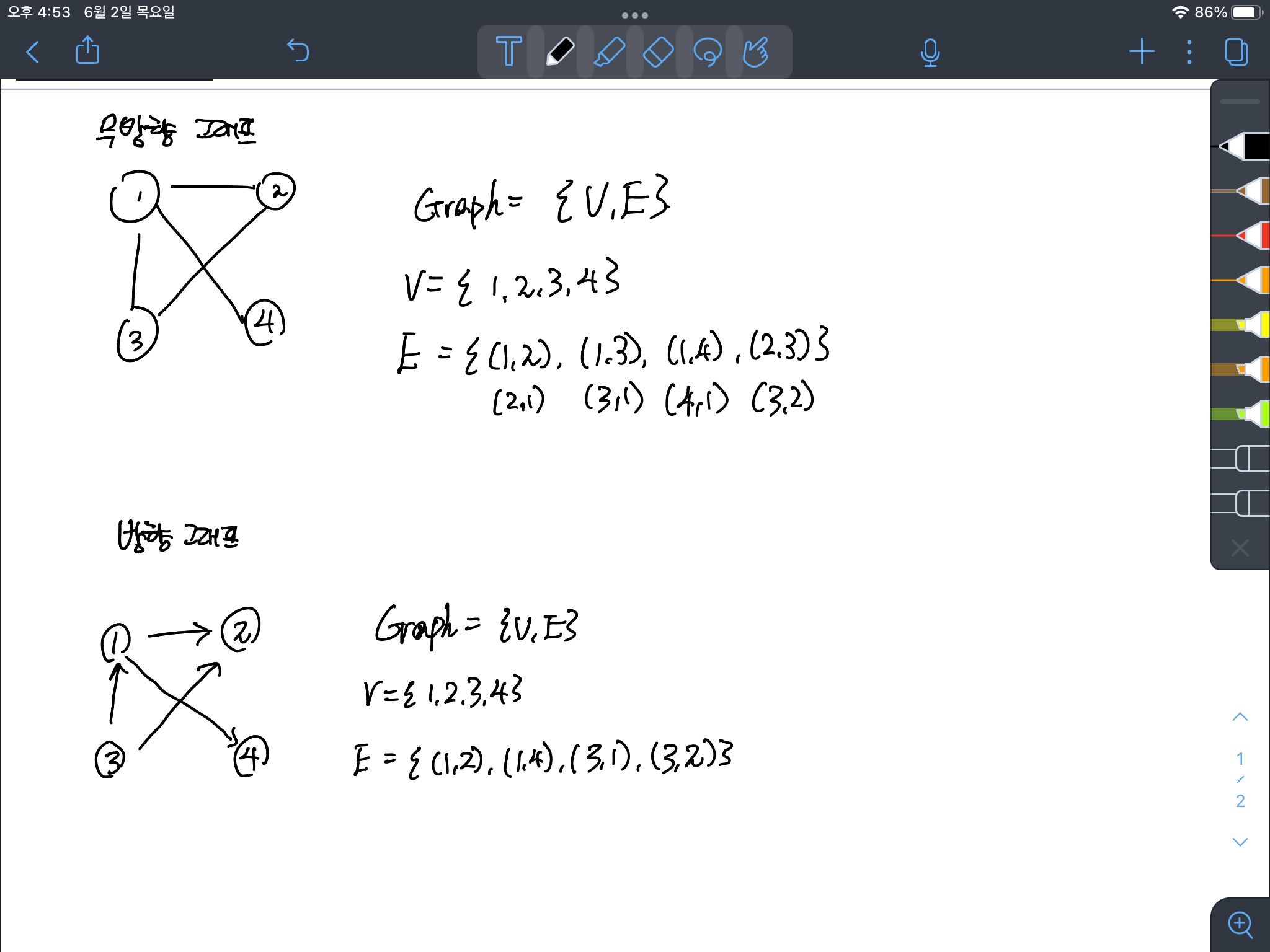
그래프에서 간선을 나타내는 방식에는 크게 두 가지가 있는데, Adjacency List와 Adjancency Matrix가 있다.

Adjacency List 방식은 각각의 노드에 대해서 인접해있는 노드 정보를 list형태로 갖고 있다.

Adjancency Matrix는 노드가 n개 일때 nXn 형태의 행렬로 표현해서 각각의 row,col 좌표에 해당하는 행렬값을 이용해서 연결여부를 저장할 수 있다.

노드 개수가 V, 간선 개수가 E일때

Type	Memory	getWeight
Adjacency Matrix	O(V2	O(1)
Adjacency List	O(E)	O(V)

각각의 방식 모두 장/단점을 가지기 때문에 상황에 맞게 적절히 이용한다.

Disjoint Set

Disjoint Set은 집합 관계를 따지기 위해 생성하는 자료구조이다. 예를 들어 노드 1, 노드 2가 같은 cycle안에 있는 지 확인 하기 위해서는 각각으로부터 DFS/BFS로 경로가 있는지를 확인해야 하는 데, 이렇게 하면 복잡하다. Disjoint set는 각각의 노드를 관리할 때 부모 노드를 이용한다. 만약 같은 부모노드로 부터 나오면 이는 같은 cycle안에 존재한다는 것을 의미하고, 2개의 disjoint set을 합칠때도 부모 노드끼리 서로 합치면 된다.

예시를 통해, disjoint set이 어떻게 작동하는지 알아보자.

Example

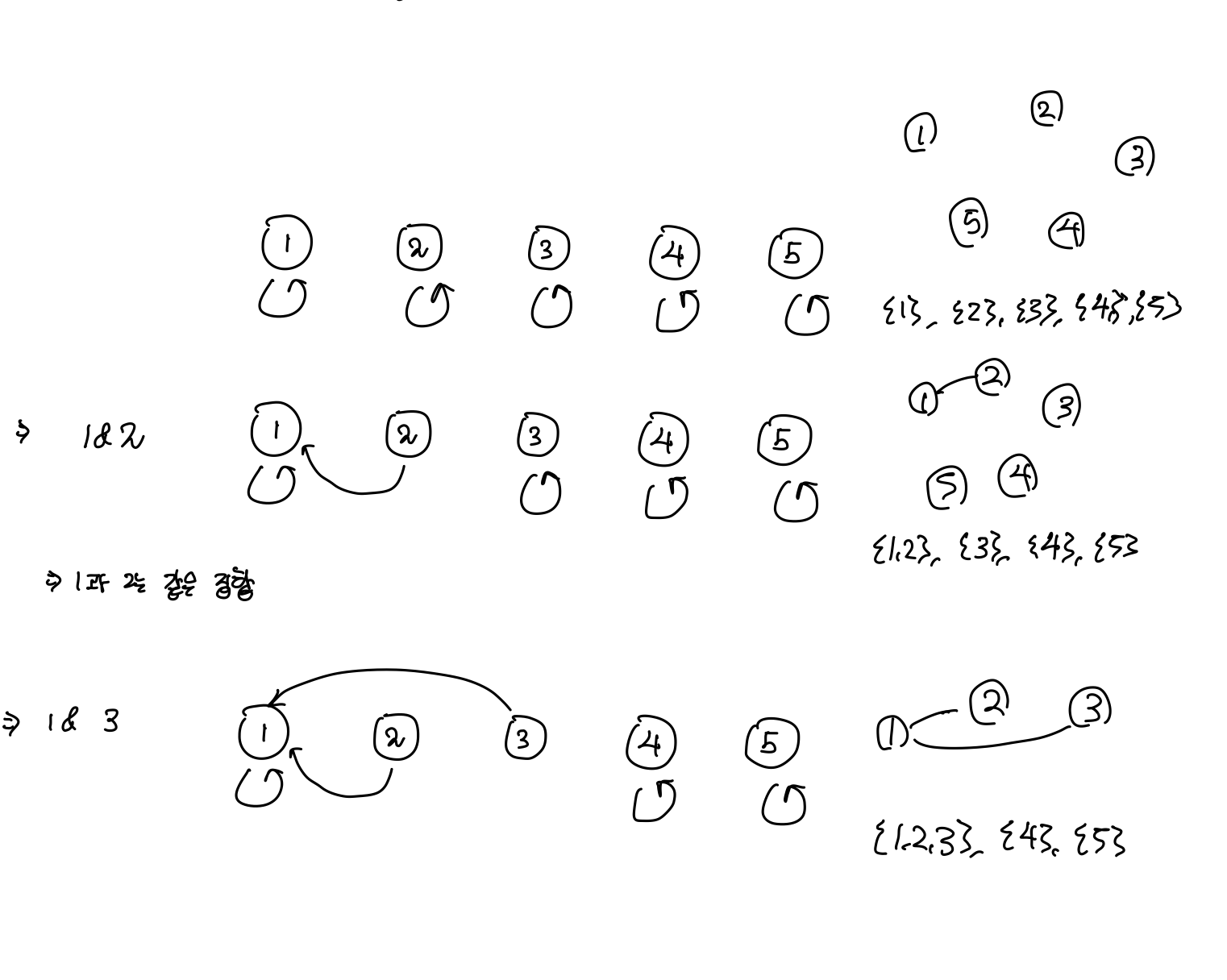
처음에는 모든 노드의 부모 노드는 자기 자신이다. 이때, 두개의 노드를 합치는 작업(간선을 추가하는 작업)을 진행하게 되면, 한쪽 노드의 부모 노드가 변경되게 된다.

만약 이 상황에서 2,3을 잇는 간선을 추가하게 된다면 어떻게 될까, 2의 부모 노드는 1, 3의 부모 노드 또한 1이다. 같은 부모 노드를 가지는 두 노드를 연결하게 되면 cycle이 생성된다. 이렇게 disjoint set을 이용하게 되면 cycle 여부를 쉽게 파악 할 수 있다.

Disjoint Set에서 쓰이는 알고리즘은 아래와 같다.

find_parent

def find_parent(parents,x):
  if x!=parents[x]:
    return find_parent(parents,parents[x])
  return parents[x]

union_parent

def union_parents(parents,x,y):
  pre_x=find_parent(parents,x)
  pre_y=find_parent(parents,y)

  if pre_x < pre_y:
    parents[pre_x]=pre_y
  else:
    parents[pre_y]=pre_x

위와 같이 알고리즘을 구현한 경우 문제점이 발생하게 되는데

Example

4,5
3,4
2,3
1,2

위와 같이 입력이 들어왔다고 가정하면 parent 관계는 아래와 같게 된다. 1<-2<-3<-4<-5 이처럼 깊이가 긴 Tree가 생성된다. 하지만 이는 매우 비효율적이게 된다.

5의 최종 부모노드를 알아내기 위해서는 5단계를 거치게 된다. 이를 해결하기 위해 경로 압축개념을 대입한다.

find_parent_compressed

def find_parent_compressed(parents,x):
  if x!= parents[x]:
    parents[x]=find_parent_compressed(parents,parents[x])
  return parents[x]

이렇게 하면 1<-2 1<-3 1<-4 1<-5

Tree가 생성되어 부모 노드 파악이 쉬워진다.

Minimum Spanning Tree

이 개념은 그래프에서 모든 노드를 유지한 채, 해당 그래프를 Tree로 바꾼다, 이때 edge의 weight의 총합이 최소가 되도록하는 것이다.

MST를 구하기 위한 알고리즘은 대표적으로 Kruskal, Prim, Solin 알고리즘이 있는데, 보통 사용하는 방시에는 kruskal, prim 알고리즘이 있다.

Kruskal Algorithm

이는 모든 간선을 집합으로 저장한 다음 이를 weight 기준으로 오름차순 정렬한 다음에 weight가 작은 순서 대로 간선을 추가하는데, 이때 간선을 추가함으로써 cycle이 생성되면 해당 간선은 넘어간다.

Source

import heapq

def find_parent_compressed(parents,x):
  if x!= parents[x]:
    parents[x]=find_parent_compressed(parents,parents[x])
  return parents[x]

def union_parents(parents,x,y):
  pre_x=find_parent(parents,x)
  pre_y=find_parent(parents,y)

  if pre_x < pre_y:
    parents[pre_x]=pre_y
  else:
    parents[pre_y]=pre_x

def kruskal(v,edges):
  #간선 집합 정령
  edges.sort()
  MST=[[] for _ in range(v+1)]
  parents=[0] * (v+1)
  for i in range(1,v+1):
    parents[i]=i
  result=0
  edge_count=0
  while edge_count<v-1:
    cost,v1,v2=edges.pop(0)

    #cycle 여부를 확인하기 위해 disjoint_set을 이용한다.
    if find_parent_compressed(parents,v1) != find_parent_compressed(parents,v2):
      union_parent(parents,v1,v2)
      result+=cost
      MST[v1].append(v2)
      MST[v2].append(v1)
      edge_count+=1
    else:
      continue
  return MST,result

Prim Algorithm

시작점 노드를 하나 설정하고, 각각의 노드에 도달하기 위한 distance 리스트를 유지한다. 만약 현 시점에서 도달할 수 없으면 무한대로 설정한다. 현 시점에서 가장 가까운 노드에 도달하는 간선을 추가하고, 노드를 추가하므로써 다른 노드들에 대한 거리 정보가 바뀌게 되면 distance 리스트를 최신화 시켜준다. 모든 노드를 추가할 때까지 해당 작업을 반복한다.

현 시점에서 가장 작은 값을 가져온다 –> heap를 이용한다.

Source

import heapq
from math import inf
def prim(start):
  distance=[inf]*n
  visited=[False]*n
  MST=[[] for _ in range(n)]
  heap=[]
  result=0

  n_vertex=1
  distance[start]=0
  visited[start]=True
  heapq.heappush(heap,(0,start))

  while n_vertex <n-1:
    weight,vertex=heapq.heappop(heap)

    for cost,adj_vertex in graph[vertex]:
      if visited[adj_vertex]:
        continue
      
      if cost < distance[adj_vertex]:
        distance[adj_vertex]=cost
        result += cost
        path[adj_vertex]=vertex
        MST[vertex].append(adj_vertex)
        heapq.heappush(heap,(cost,adj_vertex))
  return MST,cost

Topological Sorting

Topological Sorting(위상정렬)은 그래프의 방향성을 유지하면서 순서대로 정렬하는 것이다.

예를 들어 아래와 같은 선수과정이 있는 수강과목이 있다고 가정할떄,

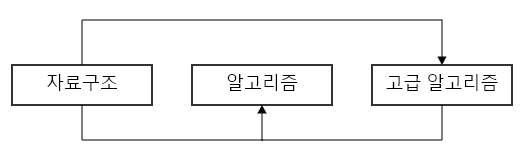
이를 위상정렬은 진행해보면 아래와 같이 나올 수 있다.

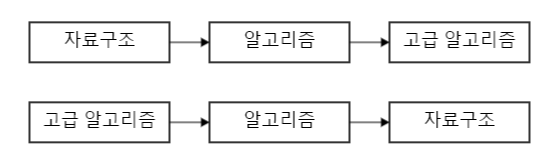
Source

from collections import deque

def topological_sort(v,graph,indegree):
  queue=deque()
  sorted_list=[]

  #진입차수가 0인 노드에서 시작이 가능하다. --> 아무런 선수 조건 없음
  for i in range(1,v+1):
    if indegree[i]==0:
      queue.append(i)
  
  #선수 조건을 하니씩 취하면서 뒤에 따라오는 후조건들을 제거해보면서 이를 다시 큐에 넣고 진행한다.
  while queue:
    vertex=queue.popleft()
    sorted_list.append(vertex)
    for adj_vertex in graph[vertex]:
      indegree[adj_vertex]-=1

      if indegree[adj_vertex]==0:
        queue.append(adj_vertex)

  return sorted_list


if __name__ == "__main__":
  v,e=0,0
  graph=[]
  indegree=[]
  with open("data2.txt") as file:
    v,e=map(int,file.readline().split())
    graph=[[] for _ in range(v+1)]
    indegree=[0]*(v+1)
    for _ in range(e):
      v1,v2=map(int,file.readline().split())
      graph[v1].append(v2)
      #topological sorting에서는 이 진입차수를 이용한다.
      indegree[v2]+=1
      
  print(topological_sort(v,graph,indegree))

Question Type

그래프 유형에서는 보통 MST 문제와 disjoint_set문제가 많이 활용된다. disjoint_set같은 경우는 그래프 뿐만 아니라, 집합관계를 다루는 문제들에서 종종 활용된다.